836. Rectangle Overlap

题目

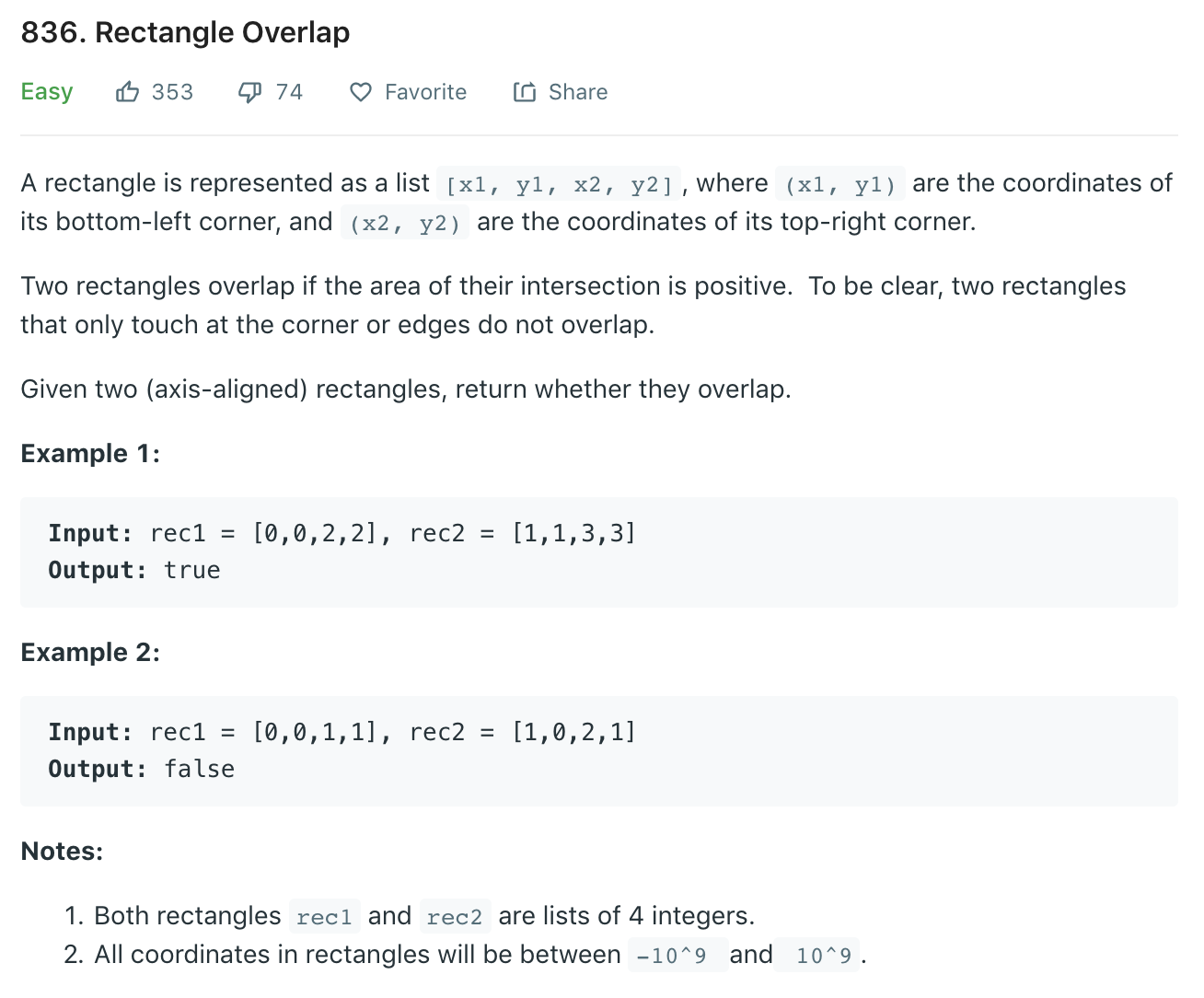
题意分析

本题需要判断两个矩形是否相交。

本题考点

判断矩形相交

解法I - 正推法

本题第一直觉，通过画矩形来罗列各种情况，来判断矩形是否相交。

整体分两种情况，一种是第二个矩形有顶点在第一个矩形内部；另一种是第二个矩形的顶点在第一个矩形边上。

如图所示：

解法I - 实现

太复杂了不实现了(╯‵□′)╯︵┻━┻

解法II - 逆推法

当我们发现正向思维太复杂，我们可以通过逆向思维思考，什么情况下两个矩形相离。

这次相对来说比较容易，只要两个矩形的某些边界相切或相离，这两个矩形必定相离，如图所示：

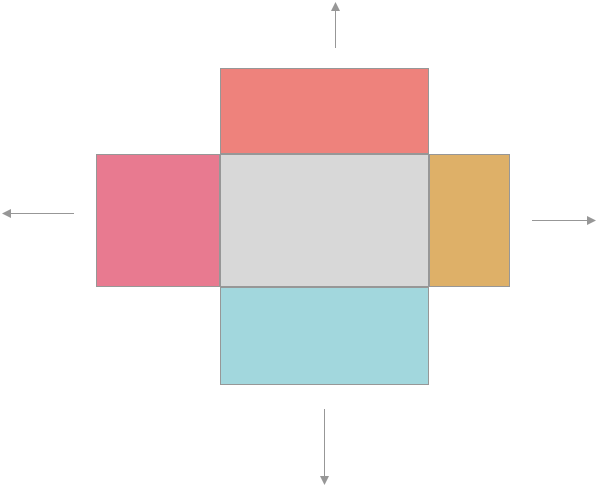
上下左右四个矩形只要和中间的矩形相切，即使往箭头标注的方向移动，这两个矩形也必定相离。

实现

class Solution {
  public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
    int x1 = rec1[0], y1 = rec1[1], x2 = rec1[2], y2 = rec1[3];
    int x3 = rec2[0], y3 = rec2[1], x4 = rec2[2], y4 = rec2[3];

    return !(x3 >= x2 || y3 >= y2 || x4 <= x1 || y4 <= y1);
  }
}

解法III - 正面推

仔细一看解法发现!(x3 >= x2 || y3 >= y2 || x4 <= x1 || y4 <= y1)实际等同于(x3 < x2 && y3 < y2 && x4 > x1 && y4 > y1)！

从逻辑上验证没问题，因此从道理上讲，正面硬刚应当也不是很困难。

想象两张纸，无论两张纸怎么放，只要有重叠，那么一定是一张纸的右边要大于另一张纸的左边，同时这张纸的左边要小于另一张纸的右边。 同理，一张纸的上边一定要小于另一张纸的下边，同时这张纸的下边一定要大于另一张纸上边。

因此：

实现

class Solution {
    public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
        return (
          rec1[2] > rec2[0] &&
          rec1[3] > rec2[1] &&
          rec1[0] < rec2[2] &&
          rec1[1] < rec2[3]
        );
    }
}