题目
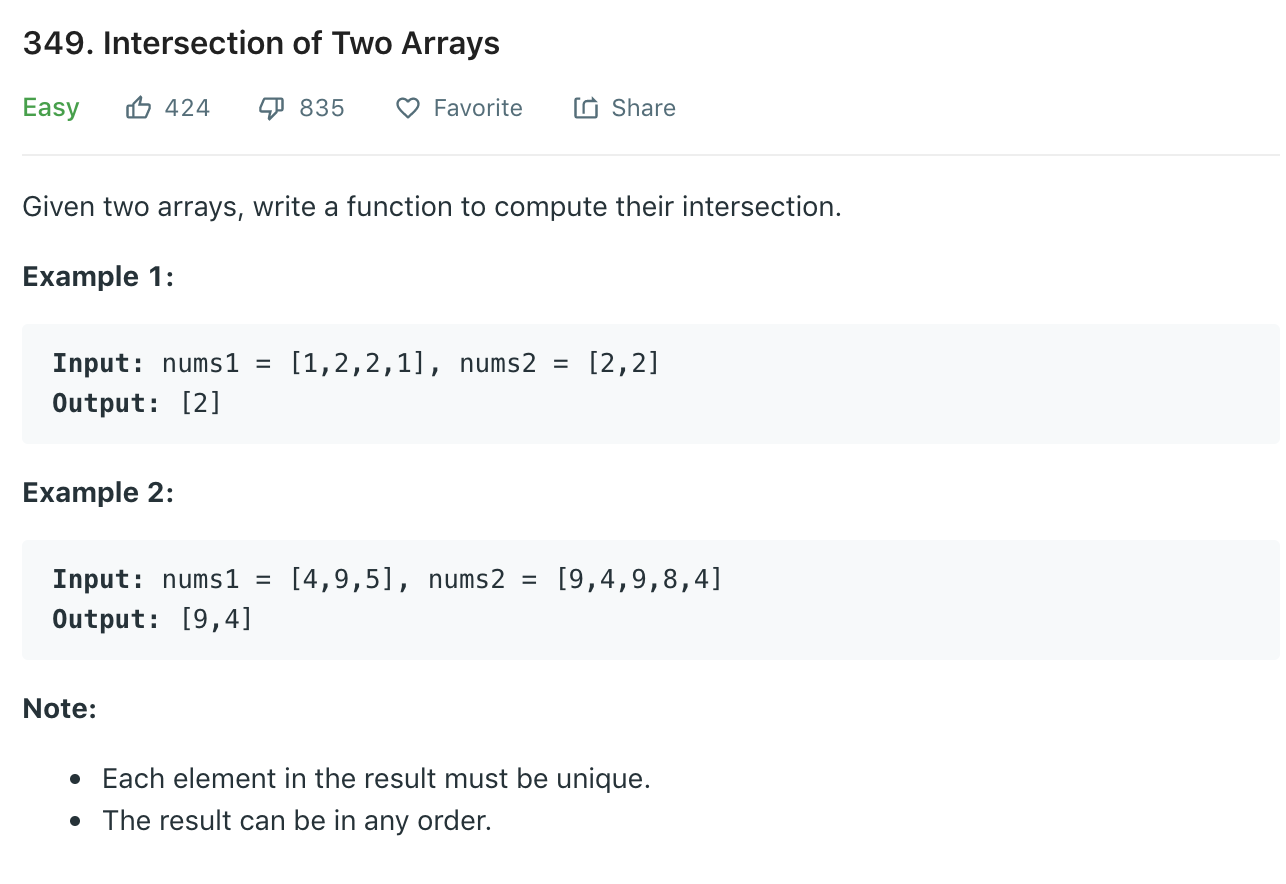
P349
P350
题意分析
这两道题的本质是一样的,我们把它们放在一起说。
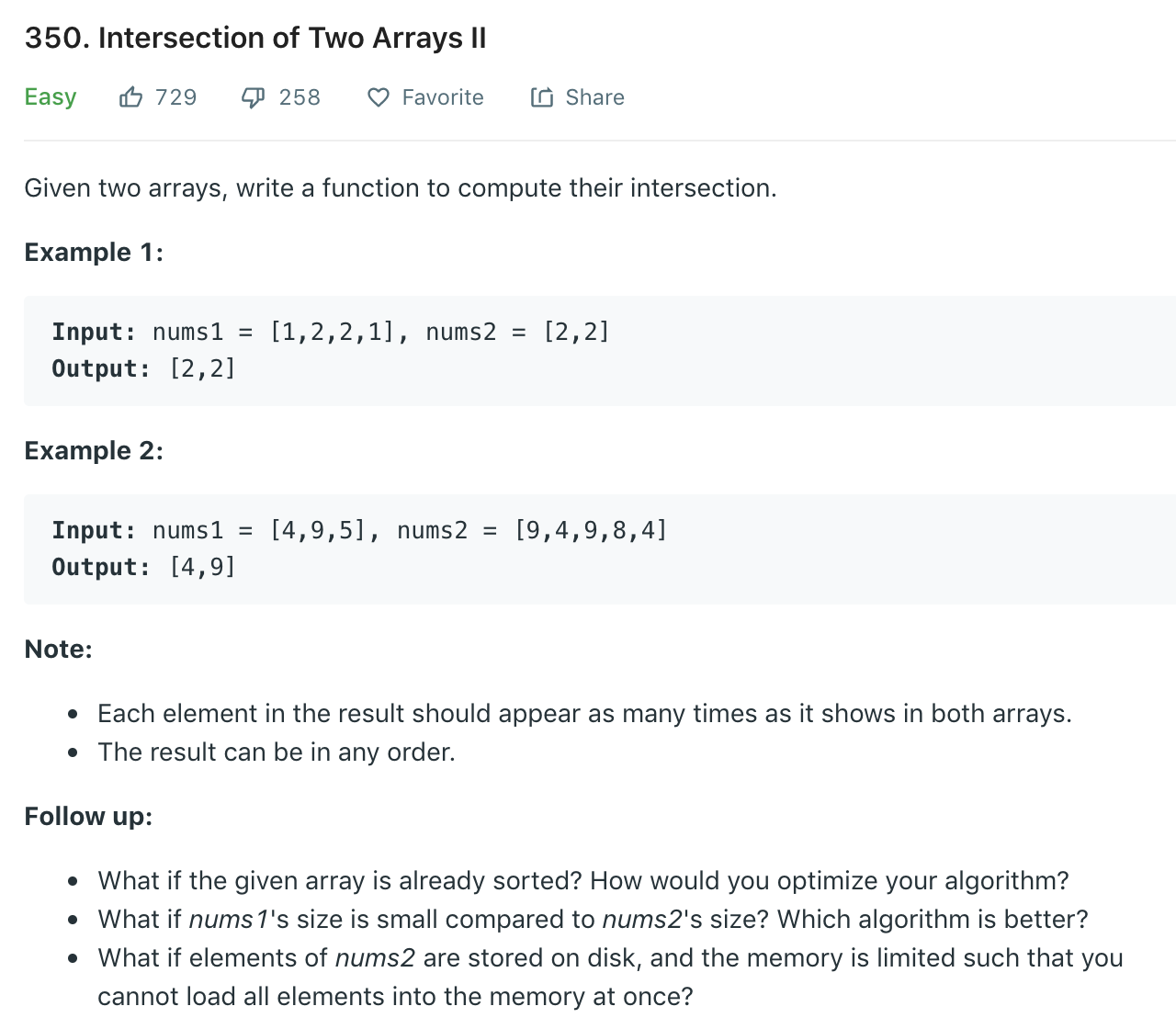
两道题都是要求两个数组的交集,区别在于,两道题目要求输出的内容不一样。
P349中,需要输出不重复的值;P350中,如果结果中有重复的元素,那也一起输出来。
同时在P350的最后,题目也提出了三个很有意思的问题:
- What if the given array is already sorted? How would you optimize your algorithm?
- What if nums1’s size is small compared to nums2’s size? Which algorithm is better?
- What if elements of nums2 are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once?
我们跳出这两道题,讲讲如果面试碰到了这个问题,面试官会怎么考。
第一问: 请写一个函数,求出两个数组的交集(p350)
思路
在我们碰到一个问题的时候,首先要在脑海中过一下这个问题的输入和输出。
输入是任意两个数组,输出是这两个数组的交集,也是一个数组。
这个问题,我们第一直觉就是暴力搜索:
解法I: 暴力搜索
遍历两个数组,如果有一样的,就加在结果集里面,显然,时间复杂度O(N2)
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
List<Integer> resultArrayList = new ArrayList<>();
// 考虑到有相同元素的情况,比如[1,2,2,1]和[2,2]
// 我们需要用一个数组记录一下,是否将这个元素已经加入结果集了
// 如果不记录的话,[1,2,2,1]&[2,2] 和 [1,2,2,1]&[2]的结果将会相同
List<Boolean> hasAddedNums2Elements = new ArrayList<>();
for (int num2: nums2) {
hasAddedNums2Elements.add(false);
}
for (int num1 : nums1) {
for (int j = 0; j < nums2.length; j ++) {
// 如果第一个数组里的元素在第二个数组里有,并且第二个数组的这个元素还没被用过
// 那么我们加入结果集,同时把第二个数组的这个元素标记为true(已用过)
if (num1 == nums2[j] && !hasAddedNums2Elements.get(j)) {
resultArrayList.add(nums2[j]);
hasAddedNums2Elements.set(j, true);
break;
}
}
}
// 将结果集的ArrayList转换为数组
int[] result = new int[resultArrayList.size()];
int pointer = 0;
for (Integer num : resultArrayList) {
result[pointer++] = num;
}
return result;
}
}
写完了上面这个程序,我们运行一看,只击败了14.53%的用户,这太难过了_(:з」∠)_
我们观察上面这个程序,发现,既然已经标注了第二个元素是否被使用,我们根本没有必要把这个元素加进去,如果第二个数组里的元素被使用了,说明他就一定在交集里面,我们优化一下:
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
List<Boolean> hasAddedNums2Elements = new ArrayList<>();
for (int num2: nums2) {
hasAddedNums2Elements.add(false);
}
// 我们定义一个变量来记录结果集的长度,用来定义int数组
int intersectionLength = 0;
for (int num1 : nums1) {
for (int j = 0; j < nums2.length; j ++) {
if (num1 == nums2[j] && !hasAddedNums2Elements.get(j)) {
hasAddedNums2Elements.set(j, true);
intersectionLength ++;
break;
}
}
}
int[] result = new int[intersectionLength];
int pointer = 0;
for (int i = 0; i < hasAddedNums2Elements.size(); i ++) {
if (hasAddedNums2Elements.get(i)) {
result[pointer ++] = nums2[i];
}
}
return result;
}
}
解法II:哈希表
运行完咱们的优化版,发现时间并没有任何变化。当然没有变化,时间复杂度还是O(N2),我们继续优化。
我们想一下上面的思路,O(N2)的原因在于,每次在找1的元素是否在2中时,我们都从头遍历了一次2,如果我们能够把遍历2这个操作给优化成O(1),那整个算法就是O(N)了。
在这里我们需要借助哈希表。
凡是涉及到去重,取数等操作的问题,首先想一想哈希表是否能够派上用场。
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
// 我们定义一个哈希表,首先进行初始化
// 每碰到一个1中的元素,我们就让其对应的值加1
// 初始化完毕后,哈希表中的值,对应的是该元素在1中出现的次数
Map<Integer, Integer> hashmap = new HashMap<>();
for (int num : nums1) {
Integer times = hashmap.get(num);
if (times != null) {
hashmap.put(num, times + 1);
} else {
hashmap.put(num, 1);
}
}
List<Integer> resultArrayList = new ArrayList<>();
// 我们接下来遍历2中的元素
// 每碰到一个2中的元素,如果他在哈希表中出现,我们就把他对应的值-1,并把这个元素加入结果集中
// 当哈希表中的值为0的时候,说明1中已经没有这个元素了,就没必要加入结果集了
for (int num : nums2) {
Integer times = hashmap.get(num);
if (times != null && times > 0) {
resultArrayList.add(num);
hashmap.put(num, times - 1);
}
}
int[] result = new int[resultArrayList.size()];
for (int i = 0; i < resultArrayList.size(); i++) {
result[i] = resultArrayList.get(i);
}
return result;
}
}
本算法时间复杂度在理想情况下(数据无哈希碰撞)为O(N),空间复杂度O(N),算是非常理想的解决方案了。
第二问,在第一问的基础上将上一问的结果集去重(p349)
思路
当面试的时候,开开心心的把哈希算法写出来之后,面试官说:”可以啊,那如果要求结果集输出不重复的元素呢?”,比如[1,2,2,1]和[2,2],结果集应该是[2,2]。
你在这里会心一笑,上一步我们为了让他显示重复的元素,才在初始化的时候把出现的次数加进来了,这次我们不需要统计出现的次数,直接在初始化时置1即可。
另外我们在上一步的基础上再进一步优化,为了减少哈希碰撞的概率,以及初始化时的操作次数,我们将以元素少的那个数组建哈希表。
同时,当两个数组至少有一个为空时,直接返回。
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
if (nums1.length == 0 || nums2.length == 0)
return new int[0];
if (nums1.length >= nums2.length) {
return calculateIntersection(generateHashMap(nums2), nums1);
} else {
return calculateIntersection(generateHashMap(nums1), nums2);
}
}
private Map<Integer, Integer> generateHashMap(int[] nums) {
Map<Integer, Integer> hashmap = new HashMap<>();
for (int num : nums) {
hashmap.put(num, 1);
}
return hashmap;
}
private int[] calculateIntersection(Map<Integer, Integer> hashmap, int[] nums) {
List<Integer> resultArrayList = new ArrayList<>();
for (int num : nums) {
if (hashmap.containsKey(num)) {
resultArrayList.add(num);
hashmap.remove(num);
}
}
int[] result = new int[resultArrayList.size()];
for (int i = 0; i < resultArrayList.size(); i++) {
result[i] = resultArrayList.get(i);
}
return result;
}
}
第三问: 上面两个都是无序数组,如果两个数组都是有序递增数组,算法该如何调整呢?
思路
看到这里又很开心,上面要有哈希表的原因,就是因为无序数组。这次都改成有序了,我们还省的用哈希表了。
对于这类两个有序数组进行操作的问题,首先考虑双指针,其次是二分法,严格来说二分法也是双指针法的一种。
所谓双指针,其实就是让两个变量先指向两个数组的第一个元素,然后按照某种规则让两个指针移动罢了,边移动边处理我们需要的数据。
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
if (nums1.length == 0 || nums2.length == 0)
return new int[0];
// 我们首先对两个数组排序
sort(nums1, 0, nums1.length - 1);
sort(nums2, 0, nums2.length - 1);
// 创建一个hashset记录我们的结果
Set<Integer> resultSet = new HashSet<>();
// p1 与 p2分别对应nums1和nums2的下标
// 因为是有序数组,我们只需要记录相等的情况即可
// 当nums1[p1] < nums2[p2]时,我们只有移动p1才可能让nums1[p1]的值再度与p2相等,反之亦然
int p1 = 0, p2 = 0;
while (p1 != nums1.length && p2 != nums2.length) {
if (nums1[p1] < nums2[p2]) {
p1++;
} else if (nums1[p1] > nums2[p2]) {
p2++;
} else {
resultSet.add(nums1[p1]);
p1++;
p2++;
}
}
int[] result = new int[resultSet.size()];
int pointer = 0;
for (int num : resultSet) {
result[pointer++] = num;
}
return result;
}
private void sort(int[] nums, int begin, int end) {
if (begin < end) {
int partitionIndex = partition(nums, begin, end);
sort(nums, begin, partitionIndex - 1);
sort(nums, partitionIndex + 1, end);
}
}
private int partition(int[] nums, int begin, int end) {
int pivot = nums[end];
int i = begin - 1;
for (int j = begin; j < end; j++) {
if (nums[j] <= pivot) {
i++;
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
int temp = nums[i + 1];
nums[i + 1] = nums[end];
nums[end] = temp;
return i + 1;
}
}
上一个算法中,我们通过双指针,操作两个有序数组得到最终的结果,整体时间复杂度是O(NlogN),也就是排序的时间复杂度。
我们上面说到,这种有序数组也可以通过二分法进行实现,我们这次只排序一个数组,并通过二分查找法来筛选我们的元素。
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
if (nums1.length == 0 || nums2.length == 0)
return new int[0];
if (nums1.length >= nums2.length) {
sort(nums2, 0, nums2.length - 1);
return calculateIntersection(nums2, nums1);
} else {
sort(nums1, 0, nums1.length - 1);
return calculateIntersection(nums1, nums2);
}
}
private int[] calculateIntersection(int[] sortedNums, int[] nums) {
Set<Integer> resultSet = new HashSet<>();
// 遍历另一个没排序的数组,二分搜索有序数组,找到了就加进结果集
for (int num: nums) {
int left = 0, right = sortedNums.length - 1;
int index = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (sortedNums[mid] < num) {
left = mid + 1;
} else if (sortedNums[mid] > num) {
right = mid - 1;
} else {
index = mid;
break;
}
}
if (index != -1) {
resultSet.add(num);
}
}
int[] result = new int[resultSet.size()];
int pointer = 0;
for (int num : resultSet) {
result[pointer++] = num;
}
return result;
}
private void sort(int[] nums, int begin, int end) {
if (begin < end) {
int partitionIndex = partition(nums, begin, end);
sort(nums, begin, partitionIndex - 1);
sort(nums, partitionIndex + 1, end);
}
}
private int partition(int[] nums, int begin, int end) {
int pivot = nums[end];
int i = begin - 1;
for (int j = begin; j < end; j++) {
if (nums[j] <= pivot) {
i++;
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
int temp = nums[i + 1];
nums[i + 1] = nums[end];
nums[end] = temp;
return i + 1;
}
}
第四问: 上面的问题所有都是在内存中操作的,如果两个数组的大小,比内存的大小还要大怎么办?
先留坑,有时间再补上。
思路
提示:文件模拟分布式算法(Hadoop),或文件排序内存双指针。
FAQ
- 针对Java
ArrayListcontains函数的问题
为什么我们不推荐使用这个函数,我们首先来看一眼这个函数的定义:
/**
* Returns {@code true} if this list contains the specified element.
* More formally, returns {@code true} if and only if this list contains
* at least one element {@code e} such thatlo
* {@code Objects.equals(o, e)}.
*
* @param o element whose presence in this list is to be tested
* @return {@code true} if this list contains the specified element
* @throws ClassCastException if the type of the specified element
* is incompatible with this list
* (<a href="Collection.html#optional-restrictions">optional</a>)
* @throws NullPointerException if the specified element is null and this
* list does not permit null elements
* (<a href="Collection.html#optional-restrictions">optional</a>)
*/
boolean contains(Object o);
当这个list包含指定的元素,返回true, 否则返回false。也就是说,当这个函数找不到一个元素的时候,需要遍历整个数组,整个函数的效率是O(N)而不是O(1)。
那么在最坏的情况下,每次循环使用contains而不是哈希表判断一个元素是否存在,都要再遍历一次数组,导致整个算法的效率下降。
我们通过使用哈希表,进行了空间换时间的操作,提升了速度,但也增大了内存的消耗。