231. Power of Two

题目

题意分析

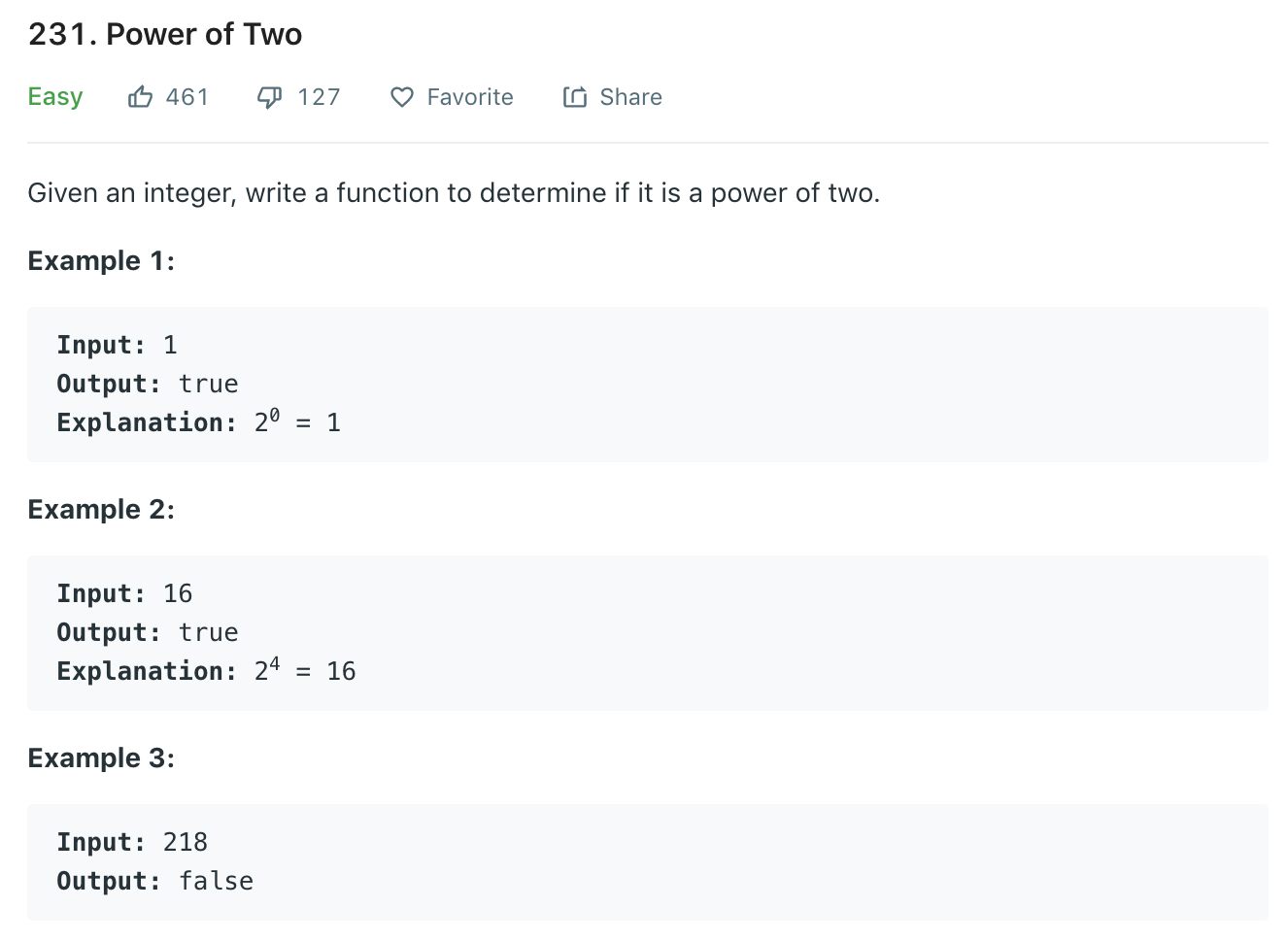
本体需要判断一个整数是否是2的幂。

本题考点

判断二的次幂。

解法I - 位运算判断法

我们首先来考虑特殊情况，当一个整数为负数或者0的时候，他就不可能是2的幂。

也就是说只有一个整数是正数的时候，他才能够是2的幂。

我们来观察一下2的幂:1, 2，4，8，16，32等

对应的二进制为1, 10, 100, 1000, 10000…

可以发现，二的幂对应的二进制中，只有一个1，剩下的全是0。

即只要这个正整数二进制中有且只有一个1，那它必定是2的幂。

我们可以通过n & (n - 1)可以去掉二进制中的倒数第一个1（参考191. Number of 1 Bits)

当我们去掉最后一个1时，如果整个二进制中没有1，说明这个二进制数只有一个1，也就是其为2的幂。

实现

class Solution {
  public boolean isPowerOfTwo(int n) {
    // 如果是负数或0，则显然不是2的幂
    
    // 去掉最后一个1，整个数为0，说明二进制中只有一个1
    // 原数字即为2的幂
    
    return (n > 0) && (n & (n - 1)) == 0;
  }
}